情况
时间:2024年7月10日8:05
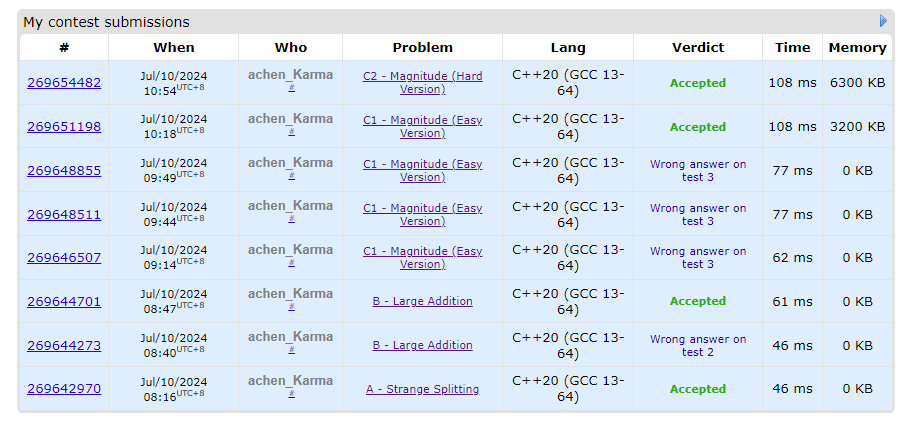
做受不了了,c1c2直接cheat了···。三个小时,结果还是这么菜。
题解
题意
一个数组的最大值和最小值之差表示这个数组的范围。
现在选中一个数组的大于一个数字涂色Blue或Red,涂色后的数组范围两者不能相同。
能有这种方案就输出YES和方案,否则输出NO
思路
数字都一样,肯定NO。找到一个数字和其他数字不一样的。把它涂R,其他都是B就行了。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| void solve()
{
int n;
cin >> n;
vector<int> a(n);
bool dif = false;
int flag = -1;
for (int i = 0; i < n; ++i)
{
cin >> a[i];
if (i >=2 && dif == false)
{
if (a[i] != a[i - 1] && a[i - 2] != a[i - 1] || a[i] != a[i - 2] && a[i - 2] != a[i - 1] || a[i] != a[i - 1] && a[i - 2] != a[i])
{
dif = true;
flag = i - 1;
}
}
}
if (!dif)
{
cout << "NO" << endl;
return;
}
cout << "YES" << endl;
for (int i = 0; i < n; ++i)
{
if (i == flag)
{
cout << "R";
continue;
}
cout << "B";
}
cout << endl;
}
|
题意
如果一个数字在 5 和 9 之间(包括 5 和 9),则它是大的。
一个正整数是大的,如果它的所有数字都是大的。
你得到一个整数 x。它可以是两个具有相同位数的大正整数之和吗?
思路
想到了每个位置都进一,然后5-9每个位相加,个位范围是0-8,其他位置都是1-9,也就是没有0。最高位肯定是1。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| {
string target;
cin >> target;
if (target[target.size() - 1] == '9' || target[0] >= '2')
{
cout << "NO\n";
return;
}
for (int i = 1;i<target.size()-1;i++){
if (target[i] == '0')
{cout << "NO\n";return;}
}
cout << "YES\n";
}
|
问题
刚开始忘了考虑中间位不能为0,wa2了。
后来发现自己还多加了个特判。没必要。
题意
c=0。对一个数组a,从头到尾
选项 1:将 c 设置为 c+ai
选项 2:将 c 设置为 |c+ai|
找到c的最大值k
思路
DP,维护最大值和最小值。
每个最大值:要么是上一个最大值直接加,要么是上一个最小值加过之后取绝对值,取两者之大。
每个最小值:是上一个最小值直接加。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| const int N = 200005;
LL dp[N][2];
void solve()
{
int n;
cin >> n;
dp[0][0] = 0;
dp[0][1] = 0;
for (int i = 1; i <= n; ++i)
{
int x;
cin >> x;
dp[i][0] = max(dp[i - 1][0] + x, abs(dp[i - 1][1] + x));
dp[i][1] = dp[i - 1][1] + x;
}
cout << dp[n][0] << '\n';
}
|
问题
别贪上头了。这题贪不得··(虽然DP的过程也是贪)·,该DP还得DP,你看看维护哪些数字可以把答案弄出来。一直WA3,搞的让人感觉能贪出来就很难受。
题意
c=0。对一个数组a,从头到尾
选项 1:将 c 设置为 c+ai
选项 2:将 c 设置为 |c+ai|
找到c最大值k,有多少种方案能得到。
思路
就是在维护最大值和最小值时,你看看上一个状态的最大值和最小值(两个值)在经过选项1或选项2的时候(两个操作),能变成下一个维护的最大值还是最小值(两个目标)。两个目标的相同数需要维护。
写8个if
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| #include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
const int N = 200005;
const LL mod = 998244353;
LL dp[N][2];
LL ways[N][2];
void solve()
{
int n;
cin >> n;
dp[0][0] = 0;
dp[0][1] = 0;
for (int i = 1; i <= n; ++i)
{
ways[i][1] = ways[i][0] = 0;
int x;
cin >> x;
dp[i][0] = max(dp[i - 1][0] + x, abs(dp[i - 1][1] + x));
dp[i][1] = dp[i - 1][1] + x;
if (dp[i - 1][1] + x == dp[i][1])
ways[i][1] = (ways[i][1] + ways[i - 1][1]) % mod;
else if (dp[i - 1][1] + x == dp[i][0])
ways[i][0] = (ways[i][0] + ways[i - 1][1]) % mod;
if (dp[i - 1][0] + x == dp[i][1])
ways[i][1] = (ways[i][1] + ways[i - 1][0]) % mod;
else if (dp[i - 1][0] + x == dp[i][0])
ways[i][0] = (ways[i][0] + ways[i - 1][0]) % mod;
if (abs(dp[i - 1][0] + x) == dp[i][0])
ways[i][0] = (ways[i][0] + ways[i - 1][0]) % mod;
else if (abs(dp[i - 1][0] + x) == dp[i][1])
ways[i][1] = (ways[i][1] + ways[i - 1][0]) % mod;
if (abs(dp[i - 1][1] + x) == dp[i][0])
ways[i][0] = (ways[i][0] + ways[i - 1][1]) % mod;
else if (abs(dp[i - 1][1] + x) == dp[i][1])
ways[i][1] = (ways[i][1] + ways[i - 1][1]) % mod;
}
LL res = max(dp[n][0], dp[n][1]), ans = 0;
if (dp[n][0] == res)
ans = ways[n][0];
if (dp[n][1] == res)
ans = (ways[n][1] + ans) % mod;
cout << ans << '\n';
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
int t;
cin >> t;
ways[0][0] = 1;
ways[0][1] = 0;
while (t--)
{
solve();
}
return 0;
}
|
问题
·····想补D,以后再说吧





